

This is a homemade solution to a problem that probably already has very thoroughly investigated solutions - how do we make a collection of triangles look like a sphere? For me, this screams immediately of solving using recursion — if some shape looks like a sphere, then we can make it look more like a sphere.
The initial shape that we start off with is the octahedron — two pyramids with their bases glued together, and we scale it so that it fits within a unit sphere. This gives us 8 initial triangles to work with.

We recursively generate more triangles from each face as follows. Each triangle has 3 midpoints along 3 of it's edges. We call these \( m_{01}, m_{02}, m_{12} \). We then lift these midpoints so they touch the surface of the sphere — in other words we normalise them. We can then form 4 new triangles from the midpoints and the existing vertices. It's easier to see this on a diagram:
p0 p0
/\ /\
/ \ / \
/ \ => m01 /....\ m02
/ \ / \ / \
/________\ /___\/___\
p1 p2 p1 m12 p2
Because this algorithm subdivides triangles based on the midpoints of their edges, we call this edge subdivision. Below we visualise the results of running it twice:


We can repeat this procedure on the triangles until we run out of memory/patience or we reach a certain depth \( d \). This algorithm generates \( 8 * 4^d \) triangles at the end. The number of triangles generated throughout the lifetime is similarly, \( 8( 4^1 + 4^2 + \ldots + 4^d ) \) which fortunately still works out to \( \Theta( 4^d ) \).
Running it with \( d = 4 \) gives something that looks a lot like a sphere, as shown below, while running it with \( d = 3 \) gives an aesthetically pleasing "chunky" sphere (first diagram on the page).

An alternative to edge subdivision is midpoint subdivision. This is a variant which lifts only one midpoint on the triangle, and creates two new triangles. The tricky thing about this algorithm is how you define the points for the new triangles:
p0 p0
. .
/ \ /|\
/ \ => / | \
/ \ / | \
/_______\ /___|___\
p1 p2 p1 m p2
The algorithm should generate two new triangles \( (m, p_0, p_1) \) and \( (m, p_2, p_1) \), instead of the more natural \( (p_0, p_1, m) \), \( (p_0, m, p_2) \). In the first case, we make sure that the next subdivision would produce a diagonal cut, from \( m \) to \( (p_0, p_1) \) and \( (p_2, p_0) \), whereas in the second case the algorithm just keeps making cuts from \( p_0 \). A picture paints a thousand words:
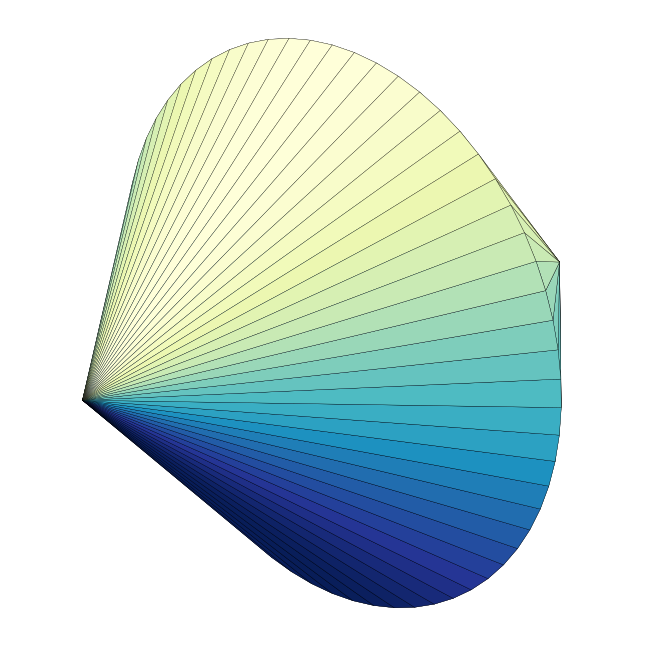

Midpoint subdivision gives us \( \Theta( 2^d ) \) triangles, so we would expect to use a higher depth for it to look more spherical. At higher depths we see the pattern of spheres drawn by the algorithm - it contains more obtuse and scalene (thin and wide) triangles compared to that of edge subdivision, which has more equilateral-looking triangles:

An advantage that it has over edge-subdivision is that the memory consumption can be controlled more easily because it grows in a factor of 2 rather than a factor of 4.
Yet another alternative is called centroid subdivision. Here, we lift the centroid \( c \) from the triangle, and then make 3 new triangles:
p0 p0
. .
/ \ /|\
/ \ => / | \
/ \ /._c_.\
/_______\ //_____\\
p1 p2 p1 p2
This was my original solution to this problem, and as we see it doesn't quite work; there are deep grooves in the surface of the sphere that cannot be fixed even at higher depths:


The lesson learnt here is that the subdivision strategies should avoid producing thin triangles. This is because intuitively there is more value in producing "fatter", regular triangles. Thin triangles, when subdivided are going to fill less of the sphere's surface, and it will be even worse when you subdivide thinner and thinner strips.
A couple more nice pictures of running hybrid algorithms - a mix between multiple algorithms:



You can get the code that generates these spheres here. Requires matplotlib. Usage example:
$ python spheres.py <method> <depth> <colormap> $ python spheres.py edge 3 YlGnBu_r $ python spheres.py centroid 3 YlGnBu_r $ python spheres.py midpoint 3 YlGnBu_r
The colormap used for the diagrams is YlGnBu_r.