An Analysis of Skip Lists

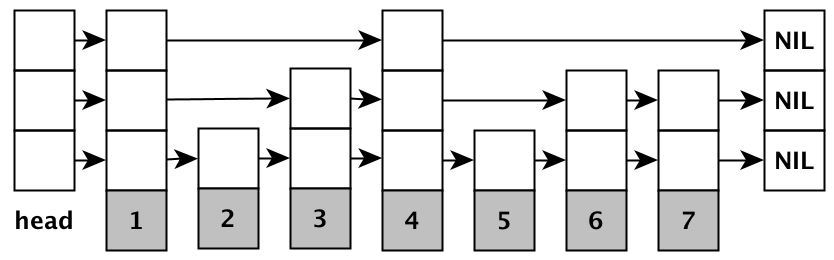
The Skip List^[1] is a probabilistic data structure that has the same average case asymptotic performance as more complex data structures such as AVL trees, balanced trees, etc. on average. The following is a hopefully more understandable probabilistic analysis, curated from various sources.

This article is not an introduction to the Skip List. For an introduction please read the original paper. Terminology here used will be borrowed from said paper.

**Figure 1:** graphical representation of a skip list.

Expected number of nodes at level $ l $

Firstly we see how to express $ L(n) $, the level at which there are $ 1/p $ nodes, in terms of $ n $. From the definition of the RandomLevel function, $ p^{l-1} $ is the probability^[2] that any given node will have an $ l $-level pointer with the lowest level being level 1^[8].

randomLevel()
  newLevel := 1
  -- random() returns a random value in [0..1)
  while random() < p do
    newLevel := newLevel + 1
  return min(newLevel, MaxLevel)

William Pugh's original RandomLevel function^[1]. Note that this function takes non-constant^[4] time.

Intuitively^[3], multiplying this by the number of nodes in the list gives us the expected number of nodes in each level: $$ \#(n, l) = n p^{l-1} $$

Finding the expression for $ L(n) $ simply requires some logarithms: $$ \begin{aligned} n p^{L(n)-1} &= \frac{1}{p} \\ n &= p^{-L(n)} \\ \lg n &= L(n) \lg \frac{1}{p} \\ L(n) &= \log_{\frac{1}{p}}{n} \end{aligned} $$

Expected length of search paths

We will now analyze the expected length of a search path, i.e. how many movements to make in order to get to any node within the list by adopting the approach of the original paper:

We analyze the search path backwards, travelling up and to the left. Although the levels of nodes in the list are known and fixed when the search is performed, we act as if the level of a node is being determined only when it is observed while backtracking the search path.

Let $ \text{cost}(k) $ denote the expected cost (the number of movements needed) for climbing up $ k $ levels in an infinite list – no matter how many leftward movements we make, we never reach the header of the list. When we reach any level $ k $ we will be able to either:

Move up a level with probability $ p $.
Move left with probability $ 1 - p $.

$$ \begin{aligned} \text{cost}(k) &= p(1 + \text{move up}) + (1 - p)(1 + \text{move left}) \\ &= p(1 + \text{cost}(k-1)) + (1 - p)(1 + \text{cost}(k)) \\ &= 1 / p + \text{cost}(k-1) \\ &= k / p \end{aligned} $$

Since we are analyzing an infinite list, we cannot use $ \text{cost}(k) $ all the way for $ n = \infty $. So we'll only use this technique until we've reached a level where we know that we have a fixed amount of nodes, independent of $ n $. Where is such a level? $ L(n) $! When we are at level $ L(n) $ we expect $ 1 / p $ nodes. It follows that the number of nodes at level $ l + L(n) $ is: $$ \frac{1}{p} \, p^l = p^{l-1} $$

Again assume that there are $ \infty $ levels after $ L(n) $, and take the pessimistic assumption that we need to traverse every node along all of the levels to the topmost level. The upper bound on the total movements required to get to the topmost level $ \infty $ is then: $$ \sum^{\infty}_{l=1}{p^{l-1}} = \frac{1}{1-p} $$

Combining this with the previous results, we use the cost function until level $ L(n) $ and add the number of movements we make afterwards, we end up with the same expression for the expected upper bound as given by the paper:

$$ \text{cost}(L(n)) + \frac{1}{1-p} = \frac{L(n)}{p} + \frac{1}{1-p} \approx O(\log n) $$

Bounding the height

We will follow the analysis given in [5], a more straightforward way to derive the asymptotic cost of traversal operations. Let $ P_l $ denote the probability of there being at least one node in a list of size $ n $ in the $ l $-th level. We have established previously that the probability of a node being in level $ l $ is given by $ p^{l-1} $: $$ P_l \leq np^{l-1}, $$

because each of the $ n $ nodes have equal chance of being part of level $ l $, and $ P_l $ is the probability of any of those $ n $ nodes being part of level $ l $. The probability of there being a node at level ($ c\log_{\frac{1}{p}}{n} + 1 $) is: $$ \begin{aligned} P_{c\log_{1/p}{n}+1} &\leq np^{c\log_{1/p}{n}} \\ &= np^{-c\log_p{n}} \\ &= nn^{-c} \\ &= \frac{1}{n^{c-1}} \end{aligned} $$

Thus we can say that the probability that the height of the tree will be lower than, say $ 3\log_{\frac{1}{p}}{n} + 1$ is given by^[6] $ 1 - 1/n^2 $. Therefore the height of the tree grows logarithmically with high probability and thus it follows that the traversal operations are also $ O(\log n) $.

Probabilistic Analysis

We now proceed to do a probabilistic analysis of the Skip List search path length - instead of just finding the expected length we can now find the probability distribution of the length. This approach is almost the same as the one in the original paper.

We will use two distributions: the binomial distribution $ B(n, p) $ and the negative binomial distribution^[9]^[10] $ NB(s, p) $. Let $ B(n, p) $ denote a random variable equal to the number of successes seen in a series of $ n $ trials each with probability of success $ p $. Similarly let $ NB(s, p) $ denote a random variable equal to the number of failures, each occurring with probability $ 1 - p $ before $ s $ successes are seen.

Let's first climb to level $ L(n) $. Intuitively we need to climb up $ L(n) - 1 $ levels, and then add a certain number of leftward movements in case there is no level above us. This number of movements is given by $ NB(L(n) - 1, p) $.

To see why, consider the following: the probability that we have to move leftwards once is $ 1 - p $. Thus $ NB(1, p) $ tells us the number of leftward movements ('failures') we have to make in order to have a level above us ('success'). Therefore the cost to climb up to level $ L(n) $ in an infinite list is: $$ (L(n) - 1) + NB(L(n) - 1, p) $$

Next let's find the remaining movements to make so that we reach the top of the header of the list. Remember that we are at level $ L(n) $ now, and the number of nodes at $ L(n) $ is given by $ B(n, 1/np) $.

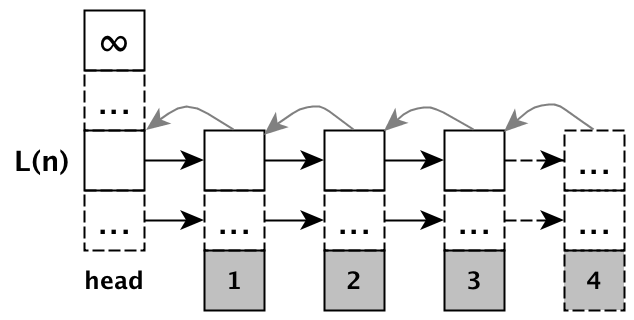
**Figure 2:** $m + 1$ leftward movements needed to reach the header.

Therefore we need to move left $ B(n, 1/np) + 1 $ times in order to reach the header of the list (refer to Figure 2 for a visual aid). Once we are there, we need to move up $ NB(1, 1-p) $ times^[11] now to reach the top of the header, and the starting point of our search. Therefore we have: $$ B(n, 1/np) + 1 + NB(1, 1-p) $$

Now we combine our results to provide an upper bound (because the negative binomial distribution can include infinite trials) on the search path length for finite lists:

$$ \begin{aligned} (L(n) - 1) + NB(L(n) - 1, p) \\ + B(n, 1/np) + 1 + NB(1, 1-p) \end{aligned} $$

The expected value of such an expression is: $$ (L(n) - 1) + \frac{(L(n) - 1)(1 - p)}{p} + \frac{1}{p} + 1 + \frac{p}{1-p}, $$

which after some rearrangement you should find that it is equal to the previous expression that we've found for the expected length of the search path, $$ \frac{L(n)}{p} + \frac{1}{1-p} $$

Avg. number of pointers per node

Finally let's warm down by looking at how to get the average number of pointers per node, which should be relatively straightforward: $$ \text{total}(n) = \sum^{\infty}_{l=1}{\#(n, l)} = n \sum^{\infty}_{l=1}{p^{l-1}} = \frac{n}{1-p} $$

To get the average number of pointers required, just divide by $ n $, in which we will end up with $ 1 / (1-p) $. The above expression also implies that the storage requirements are $ O(n) $.

[1]: William Pugh: Skip Lists: A Probabilistic Alternative to Balanced Trees

[2]: Actually the probability of there being an $ l $-level pointer when $ l \gt \text{MaxLevel} $ is zero, but let's ignore this detail for simplicity. Our analysis is pessimistic so it will be safe (and much cleaner) to take $ \text{MaxLevel} = \infty $.

[3]: Less intuitively, it's because the nodes that have a certain level are distributed according to a binomial distribution $ B(n, p^{l-1}) $, and the expected value of such a distribution is $ np^{l-1} $.

[4]: As noted in Skip Lists: Done Right, the original paper made the mistake of having level-generation take non constant time. A constant time implementation is provided in the link; here is the relevant pseudo-code for completeness:

define generate_level():
    -- First we apply some mask which makes sure that we don't get a level
    -- above our desired level. Then we find the first set bit.
    ffz(random() & ((1 << max_level) - 1))

[5]: https://www.ics.uci.edu/~pattis/ICS-23/lectures/notes/Skip%20Lists.pdf

[6]: Because $ P_l $ is the probability of there being one node at level $ l $, this means that $ P_l $ is also the probability of the list having height $ l $. Thus $ 1 - P_l $ must be the probability that the height is less than $ l $.

[8]: Starting from level 1 is easier as it allows us to easily derive the expected search path length without fussing with partial fractions, though I see the attraction in starting from level 0, which gives subjectively nicer looking equations.

[9]: https://en.wikipedia.org/wiki/Negative_binomial_distribution

[10]: John D. Cook: Notes on the Negative Binomial Distribution

[11]: We need to find the remaining number of levels above $ L(n) $. The probability of a level being above us is $ p $; modelling this situation with the negative binomial, a 'failure' occurs with probability $ p $, thus we have $ NB(1, 1-p) $ since we are interested in how many levels before we run out of levels (slightly awkward way to put it).

An Analysis of Skip Lists

Expected number of nodes at level \( l \)

Expected length of search paths

Bounding the height

Probabilistic Analysis

Avg. number of pointers per node