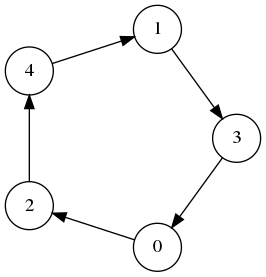
Say we place 5 items in a circle. If we count in 1s, i.e. the 1st item, then the 2nd, then the 3rd then we will count all items by the end of 5 counts. What if instead we counted by 2? This is now a bit trickier. Let's call the first item the 0th item. Then our count sequence would be like this: $$ 0, 2, 4, 1, 3 $$
So we still cover the ring of all 5 items. Notice that because we're counting in a ring we could ignore all items that are above 5; so these two count sequences are in some sense, the same:
| 0 | 2 | 4 | 6 | 8 |
| 0 | 2 | 4 | 5 + 1 | 5 + 3 |
This idea is cleanly encoded in the modulus operator: \( 8 \equiv 3 \pmod 5 \) and in general, \(p \equiv q \pmod n\) iff \( \exists a,b \in \mathbb{Z} \) s.t. \( p = an + r \) and \( q = bn + r \).

Now comes the general question: given \( n \) objects in a ring, can we cover the ring if we count by \( a \) each time? Let \( F(n, a) \) denote whether we can cover the ring of \( n \) objects counting by \( a \).
Let's get some obvious cases out of the way:
Just to warm up, we start off with this observation - if say \( n = 5 \) and \( a = 4 \), then our count sequence is: $$ 0, 4, 3, 2, 1 $$ But this is the same as the count sequence for 1 (\( 0, 1, 2, 3, 4 \)), only reversed around 0. Intuitively this makes sense - we're adding in a ring of \( n \) elements so it shouldn't matter if we count from \( n - a \) or \( a \). Let's prove it:
Claim: \( F(n, a) = F(n, n - a) \)
Proof: Consider the count sequences for \( a \) and \( n - a \):
\( 0 \) \( 0 \) \( a \) \( (n-a) \) \( 2a \) \( 2(n-a) \) \( 3a \) \( 3(n-a) \) \( \vdots \) \( \vdots \) \( (n-1)a \) \( (n-1)(n-a) \) Now let's try expanding some of the brackets; expanding the last one on the right count sequence gives us: $$ n^2 - an - n + a \equiv a \pmod n $$ This is the second element in the left count sequence. Let's try to show this holds in general. What happens if we take the \( (i+1) \)-th element from the right sequence? $$ \begin{aligned} (n-i)(n-a) &= n^2 - an - in + ia \\ &= n(n - a - i) + ia \\ &= ia \pmod n \end{aligned} $$ And so we have a one-to-one mapping between the two sequences; if one covers \( n \) then the second one covers \( n \) as well, and vice-versa. \( \Box \)
The previous result is a special case of the more general result as follows: for any \( b \), $$ F(n, a) = F(n, bn + a) $$ which can be easily proven using a similar approach. This means counting with \(a\) is the same as counting with the remainder of \( a \) mod \( n \), which eases our lives.
Now what happens if \( a \) is not a divisor of \( n \)? Let's focus on one case first - composite numbers. For instance, we know that for \( n = 16 \), we can't cover it with 2 but we can cover it with 3. Can we hope to cover it with 6? If we write out the count sequence, the answer is no, because we never touch any odd numbered objects.
Since \( a \) is a composite number we can rewrite it as \( a = pq \), with suitable values for \( p, q \) - notably, \( 1 \lt p, q \lt a \).
Claim: \( F(n, pq) = F(n, p) \land F(n, q) \)
Proof: Let's prove \( F(n, pq) \implies F(n, p) \land F(n, q) \). Examining the count sequence of \( pq \), we can express each element \( ipq \), with \( 0 \leq i \leq n-1 \) as: $$ \begin{aligned} ip &\equiv r \pmod{n} \\ q &\equiv q \pmod{n} \\ ipq &\equiv rq \equiv r' \pmod{n} \end{aligned} $$ Now the reasoning is quite subtle; if \( r' \) is different for all \( n \) values of \( i \), then \( r \) must also be different for all \( n \) values of \( i \). Thus both \( p \) and \( q \) cover \( n \).The second direction is symmetric and can be found using the same technique. \( \Box \)
Aside
Perhaps a more intuitive proof for the second direction can be given as follows. Consider the count sequences of both \( p \) and \( q \), extended to infinity. Then we have:
\( 0 \) \( 0 \) \( p \) \( q \) \( 2p \) \( 2q \) \( 2p \) \( 2q \) \( \ldots \) \( \ldots \) \( qp \) \( pq \) \( \ldots \) \( \ldots \) \( 2qp \) \( 2pq \) \( \ldots \) \( \ldots \) Then we see that the count sequence of \( pq \) is equivalent to the intersection of the count sequences of \( p \) and \( q \). The reasoning follows — if \( p \) and \( q \) both cover \( n \), then \( 0, p, 2p, \ldots (n-1) p \) generates some permutation of \( 0, 1, 2, \ldots n-1 \). This multiplied by \( q \) generates yet another permutation of \( 0, 1, 2, \ldots n-1 \) and thus also covers \( n \).
It is clear then that if one of them doesn't cover \( n \) then \( pq \) also doesn't cover \( n \). \( \Box \)
So we know that if \( a \) does cover \( n \), then the divisors of \( a \) also need to cover \( n \). If we follow this recursive argument, then we are eventually left with prime numbers. E.g.: $$ \begin{aligned} F(n, 84) &= F(n, 2) \land F(n, 42) \\ &= F(n, 2) \land F(n, 2) \land F(n, 21) \\ &\ldots \\ &= F(n, 2) \land F(n, 2) \land F(n, 3) \land F(n, 7) \end{aligned} $$ Now, we know that if any (prime) number divides \( n \) then we can't hope to cover \( n \) with said number. This implies that in order for \( a \) to cover \( n \), \( a \) needs to share no common divisors with \( n \), i.e. \( a \) and \( n \) need to be coprime. Otherwise, eventually when we break down \( a \), we would find some \( p \) to be a multiple of \( n \).
Claim: if \( a \) and \( n \) are coprime then \( a \) covers \( n \).
Proof: Consider \( a \)'s count sequence (all taken mod \( n \)): $$ 0, a, 2a, 3a, \ldots (n-1)a $$Our claim of coverage is equivalent to saying that there are no two elements that repeat themselves in this sequence.
Now assume the contrary: this sequence contains some duplicate elements \( ja \equiv ia \pmod n \), s.t. \( i \neq j \) and both \( 0 \leq i \lt j \leq n-1 \). We can rewrite them as: $$ \begin{aligned} ia &= pn + r \\ ja &= qn + r \end{aligned} $$ We can rearrange these around \( r \) and set them to be equal to each other: $$ \begin{aligned} ia - pn &= ja - qn \\ ja - ia &= qn - pn \\ a(j - i) &= n(q - p) \end{aligned} $$ Since \( j \gt i \) (it follows that \( q \gt p \)), we can rewrite \( j \) and \( q \) in terms of \( i \) and \( p \): $$ \begin{aligned} j &= i + c \\ p &= q + d \end{aligned} $$ for some \( c,d \gt 0 \). Some substitution: $$ ac = nd $$ Now we know that \( a \) and \( n \) are coprime. So we can't get rid of common multiples on both sides. Thus, any integer solutions for this equation has the form \( c = fn \) and \( d = fa \) for some \( f \in \mathbb{Z} \).
Since \( c \gt 0 \), it follows that \( f \gt 0 \) and: $$ j = i + c = i + fn \gt i + n \gt n - 1 $$ we've found our contradiction! Thus we find that the prime \( a \) does indeed cover \( n \) if \( a \) is not a multiple of \( n \). \( \Box \)
So with all these we can finally give an expression for \( F(n,a) \): $$ F(n,a) = \begin{cases} true &\text{if } n = 0, \\ true &\text{if } \gcd(n,a) = 1 \text{ and } a \neq 0, \\ false &\text{otherwise} \end{cases} $$
We have, in the end, a nice result with well-known, fast algorithms to compute an answer. The correctness of the final expression is pretty easy to show; if we pick an \( a \) which is not coprime to \( n \) then using the decomposition argument we eventually find a prime that divides \( n \).
Adapting the previous proof we can show the cycle lengths. Let \( g = \gcd(n, a) \). Then: $$ \begin{aligned} ac &= nd \\ ga'c &= gn'd \\ a'c &= n'd \end{aligned} $$ Remembering that \( c = j - i \), we see that we get cycles of length \( c = pn' \lt n \) for a maximal \( p \in \mathbb{Z}_+ \), where \( n' = n / \gcd(n, a) \).Example: \( n = 16, a = 6 \):
We expect \( c = \frac{16p}{\gcd(16, 6)} = 8p \lt 16 \). This means \( p = 1 \). $$ 0, 6, 12, 2, 8, 14, 4, 10, 0, 6, \ldots $$ The cycle length (position of second 0 - position of first 0) is 8.