Graph Algebras

This is a quick and dirty post about some thoughts I had when reading Graph Algebras by Andrey Mokhov. In the post, he describes two operators that can be used to decompose any graph into a series of operations on smaller subgraphs. An analogy is: $$ 5 = 2 + (4 - 1) $$ here + and - are the operators, and 2, 4, 1 are the subgraphs. The two operators are Overlay ($ + $) and Connect ($ \rightarrow $): $$ \begin{aligned} (V_1, E_1) + (V_2, E_2) &= (V_1 \cup V_2, E_1 \cup E_2) \\ (V_1, E_1) \rightarrow (V_2, E_2) &= (V_1 \cup V_2, E_1 \cup E_2 \cup (V_1 \times V_2)) \\ \end{aligned} $$ where $ \times $ denotes the cartesian product of two sets. For simplicity, when we have a graph that's just a single node, we would denote it by just the node itself, e.g. $ v \equiv (\{v\}, \emptyset) $. We also define $ \epsilon \equiv (\emptyset, \emptyset) $.

Note: here we will consider only undirected graphs, but in the original post and the implementation one can use this algebra for directed graphs.

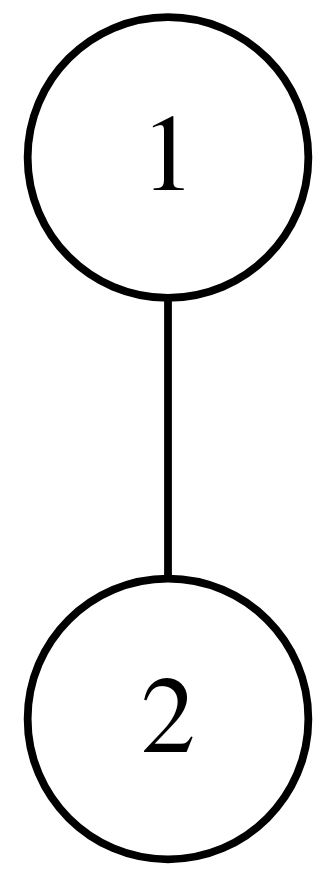
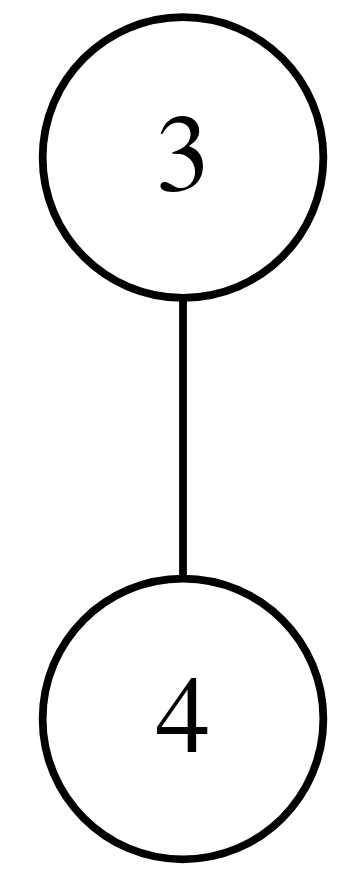
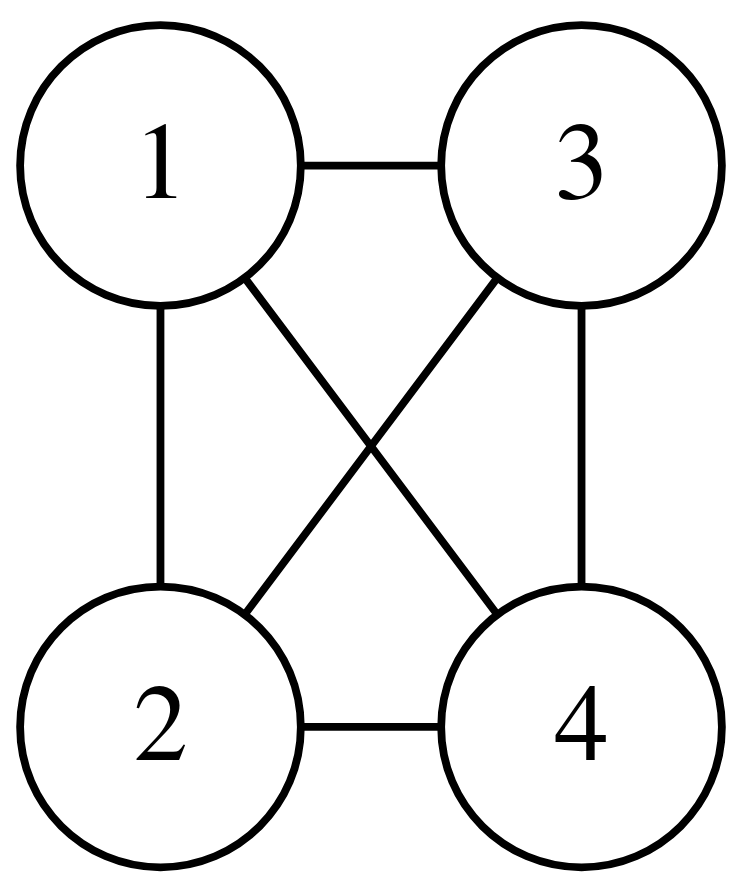
An example of a graph expressed using Overlay and Connect is the complete graph on 4 nodes — $ K_4 $, (graph with 4 nodes where every node is connected to every other node) can be defined in terms of our operators using: $$ (1 \rightarrow 2) \rightarrow (3 \rightarrow 4) $$

Or visually:


$1 \rightarrow 2$	$3 \rightarrow 4$	$(1 \rightarrow 2) \rightarrow (3 \rightarrow 4)$

It is easy to see that $ + $ and $ \rightarrow $ can produce any graph, starting from the one-vertex graph. To prove this, consider any graph $ G = (V, E) $, then the following expression is equivalent to $ G $: $$ \sum_{(u, v) \in E}{(u \rightarrow v)} $$

where $ \sum_{i=1}^{n}{a_i} $ in this context is abused to mean $ a_1 + a_2 + \ldots + a_n $. Intuitively, we just overlay all of the edges (the individual ($ u \rightarrow v $)s) on top of one another, and we get the original graph back. There is a subtle mistake though, that the above expression only works on connected graphs (where all nodes have at least one neighbour). The fix is easy: $$ (V,E) \equiv (\sum_{(u, v) \in E}{(u \rightarrow v)}) + (\sum_{v \in V}{v}) $$

But of course, doing a decomposition this way would yield no benefits for anyone trying to get a 'feel' for the graph. For instance, we could well have expressed $ K_4 $ as: $$ (1 \rightarrow 2) + (1 \rightarrow 3) + (1 \rightarrow 4) + (2 \rightarrow 3) + (2 \rightarrow 4) + (3 \rightarrow 4) $$

Which would be no better than simply listing the edges. One (possibly) open question is then the following: can we compute a 'minimal' decomposition of any graph $ G $ using the operators? Or better yet — given some decomposition of graph $ G $ using the operators, can we simplify it?

Formalisms aside, the intuitive question is this: can we get a more 'compact' decomposition? One way to start approaching this problem is by looking at the axioms of the algebra. We have the following properties:

$ G + G = G + \epsilon = \epsilon + G = G $
$ G \rightarrow \epsilon = \epsilon \rightarrow G = G $
$ x + y = y + x $
$ x \rightarrow y = y \rightarrow x $ for undirected graphs
$ x \rightarrow (y + z) = (x \rightarrow y) + (y \rightarrow z) $
$ x \rightarrow y \rightarrow z = (x \rightarrow y) + (x \rightarrow z) + (y \rightarrow z) $

Probably with quite some head scratching we can use the axioms to simplify our list of edges for $ K_4 $. But a simpler method is to use the following extra observation (simply an application of rule 5 and 6): $$ (x \rightarrow (y + z)) + (y \rightarrow z) = x \rightarrow y \rightarrow z $$

Rewriting our edge list for $ K_4 $: $$ \begin{aligned} K_4 &= (1 \rightarrow (2 + 3 + 4)) + (2 \rightarrow (3 + 4)) + (3 \rightarrow 4) \\ &= (1 \rightarrow (2 + 3 + 4) + (2 \rightarrow 3 \rightarrow 4)) \\ &= (1 \rightarrow (2 + (3 + 4)) + (2 \rightarrow (3 \rightarrow 4))) \\ &= 1 \rightarrow 2 \rightarrow 3 \rightarrow 4 \end{aligned} $$

Which turns out to be 'simpler' than our original expression! This problem probably is NP-hard, but it would be interesting to come up with heuristics to simplify decompositions. Any simplification would likely also help speed up algorithms which process the graph based on decompositions.

Cographs?

Another interesting direction is the following: consider the two operators Disjoint Union ($ \oplus $) and the Disjoint Join ($ * $); they should immediately ring bells for those who know about Cographs. They are defined very similarly as follows: $$ \begin{aligned} (V_1, E_1) \oplus (V_2, E_2) &= (V_1 \cup V_2, E_1 \cup E_2) \\ (V_1, E_1) * (V_2, E_2) &= (V_1 \cup V_2, E_1 \cup E_2 \cup (V_1 \times V_2)) \end{aligned} $$

with one very important difference: $ V_1 $ and $ V_2 $ (and by extension, $ E_1 $ and $ E_2 $) must be disjoint, i.e. $ V_1 \cap V_2 = \emptyset $.

It has been shown that any graphs constructed using the two operations (starting on the one-vertex graph) do not contain $ P_4 $ (the path on 4 vertices) as an induced subgraph (i.e. we cannot get $ P_4 $ by deleting vertices and their incident edges).

A question naturally arises: given any forbidden subgraph $ H $, does there exist a set of operators such that we cannot get $ H $ as an induced subgraph in graphs constructed using those set of operators? We must place some restrictions on those operators so that the problem doesn't get too easy; they...

cannot bound the size of the graphs they operate on. Otherwise we can just limit the size of the sets to be $ |H| - 1 $.
are only allowed to perform set operations on the graphs, e.g. intersection, union, cartesian product, difference, etc.

Even if the answer to the previous question is “not always” or the problem ends up being ill-defined, it would be interesting to see crazy constructions just to prevent say, $ C_3 $.


\(1 \rightarrow 2\)	\(3 \rightarrow 4\)	\((1 \rightarrow 2) \rightarrow (3 \rightarrow 4)\)