Problem: in a graph \( G \) of nodes \( N_1, N_2, \ldots N_n \), a celebrity is a node \( N_c \) where there is a directed edge from all other nodes to \( N_c \) but no edge from \( N_c \) to any node. Additionally, there is no edge from any node to itself in the graph. Locate the celebrity.
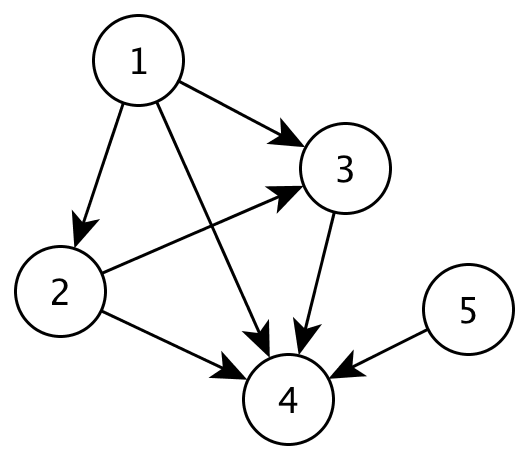
An example of such a graph with celebrity 4. It has \( n - 1 = 4 \) edges incident on it (it is known by 4 other nodes) and 0 edges from it (it knows nobody else).

Claim: There is only zero or one celebrity in \( G \).
Proof: A graph with zero celebrities can be trivially constructed. Assume there exists a graph \( G' \) with more than 1 celebrity. Let \( A, B \) be any two different celebrities. An edge must exist between any other node and a celebrity, so \( A \rightarrow B \) and \( B \rightarrow A \). However this means that \( A \) and \( B \) are not celebrities. Hence such a graph \( G' \) does not exist.
We'll first assume that there exists a celebrity in the graph (and hence, that the graph is not empty). Algorithms presented here can be easily combined so they do not make this assumption.
We can naïvely determine which node is a celebrity in \( O(n^2) \) time by brute forcing the solution and checking if there is an edge between a node and every other node in the graph:
IsCelebrity(n, G):
foreach m ≠ n in nodes(G):
if m → n does not exist or n → m exists:
return false
return true
BruteForceFind(G):
for n in G:
if IsCelebrity(n, G):
return n
But let's try to do better. One approach we can take is to assume everyone is a celebrity initially. If we can eliminate at least one node each time we check if an edge exists (we ask the nodes a question), then we can make the algorithm run in linear time.
Find(G):
C = nodes(G)
while |C| ≥ 2:
a, b = any 2 nodes from C, a ≠ b
if a → b exists:
remove a from C
else:
remove b from C
return the only item in C
Claim: Find(G) correctly returns the celebrity.
Proof: Consider what happens at each iteration. Let \( a, b \) be the two distinct nodes selected on each iteration. Two cases:
Let \( N_c \) be the celebrity. We know that \( N_c \nrightarrow N \) and \( N \rightarrow N_c \) for any other node \( N \). Thus \( N_c \) will never be removed, and the last pair to be considered is always \( (N_c, N) \). Every other node which is by definition not a celebrity will be eliminated by one of those cases, hence the algorithm will correctly return \( N_c \).
An alternative approach is to solve the problem recursively, in which a longer, but equivalent proof by induction on \( G \) can also be done if one “rephrases” the algorithm equivalently as so:
Find2(G):
if |G| == 1:
return only node in G
a, b = any 2 nodes from G, a ≠ b
if a → b exists:
G' = G - {a}
else:
G' = G - {b}
return Find2(G')
Finding the asymptotic time taken by this algorithm is simple: at each iteration one node is removed, therefore it takes \( n \) iterations for a graph of size \( n \). Assuming determining whether an edge exists is \( O(1) \), and that retrieving the nodes in our graph is \( O(1) \), the time taken is bounded by \( O(n) \).
Pedants would point out that the asymptotic bounds for the algorithms given above are not correct – they should be \( O(V) \) instead of \( O(n) \), where \( V \) is the number of vertices in the graph, but remember that in the initial problem statement \( n \) was the number of nodes in the graph. However the pedants are right! We should use \( V \) instead of \( n \) if the results are quoted elsewhere.
If we were given instead an adjacency list of size \( n \), then below is an \( O(n) \) algorithm to determine the celebrity:
FindAL(L):
W = {}
R = {}
foreach a → b in L:
remove a from W
add a to R
if b is not in R:
add b to W
return only item in W
We divide the nodes into two classes: wannabes \( W \) and rejected \( R \). It is easy to prove correctness by considering when will a node be added/removed from \( W \).
The algorithms presented assume that there is a celebrity in the graph. However they can be adapted easily for possibly empty graphs where there may be no celebrities:
MaybeFind(G):
if |G| > 0:
c = Find(G)
if IsCelebrity(c, G):
return c
return NoCelebrity
This uses the fact that Find(G) will not correctly
return a celebrity node if one does not exist — in that case it
will simply return the last remaining node that has failed to be
eliminated. The algorithm is still \( O(n) \), but with worse
constants as we need to perform an \( O(n) \) check at the end
to ensure we have a celebrity.