Disclaimer: The following entry is not about one specific thing but around multiple things that drifted into my mind while thinking about the Counting Squares problem.

There is a certain class of questions that go "How many squares can count in this \( n \) by \( n \) square"? Upon trying to count the squares in different \( n \times n \) squares we arrive at the decision that it sort of resembles the sum of \( 1, 2^2, 3^2, \ldots n^2 \).
It is easy to prove why that is the case. We will first start by trying to count the number of \( i \times i \) squares we can fit on a single \( n \times i \) row. With a bit of drawing and imagination, for the case where \( i = 2 \):
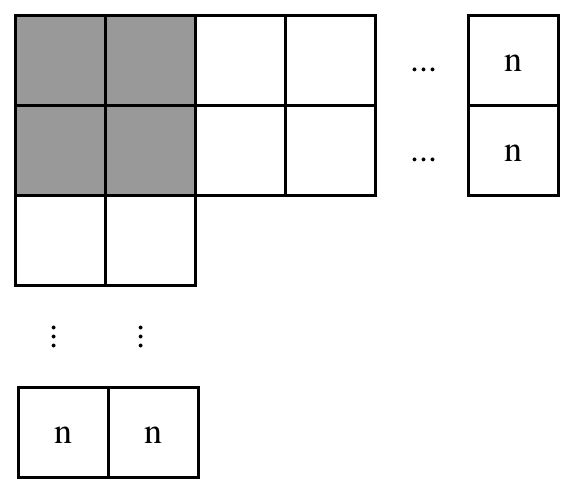
Notice that the number of other squares we can fit in this row is \( n - i \); i.e. the number of positions for the top left corner block. Therefore including the current square we have \( n - i + 1 \) possible positions. Repeating this argument for the columns, we have: $$ (n - i + 1)^2 $$
being the number of ways to fit \( i \times i \) squares on an of \( n \times n \) square. This is because for each choice of row-position to place our square we have the same number of column-positions to place it. It is clearly not possible to fit any squares of size \( \gt n \), so we can say that the total number of squares is given by the following sum: $$ \sum_{i=1}^{n}{(n-i+1)^2} = \sum_{i=1}^{n}{i^2} = \frac{n(n+1)(2n+1)}{6} $$
For an \( n \times m \) shape we would have to change the formula to the slightly uglier, but nonetheless beautiful: $$ \sum_{i=1}^{\min{(n,m)}}{(n-i+1)(m-i+1)} $$
The problem can also be generalised to arbitrary dimensions: for 1 dimension the question is:
How many contiguous chunks could be found in a chunk of length \( n \)?Since this is the same thing as the analysis we did for the rows of an \( n \times n \) square it is just \( \sum_{i=1}^{n}{i} \). For 3 dimensions we would have to consider for the z-axis; but that is simple enough: $$ \sum_{i=1}^{n}{i^3} $$
For each extra dimension we add one more degree of freedom (always wanted to use that word). So for an \( n \times n \times n \times \ldots \times n \) (\( d \) times) shape, the number of smaller \( d \)-dimensional regularly sized chunks we can find is given by: $$ \sum_{i=1}^{n}{i^d} = \Theta(n^{d+1}) $$